문제링크
https://www.acmicpc.net/problem/11729
문제
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로 옮기려 한다.
- 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
- 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.
이 작업을 수행하는데 필요한 이동 순서를 출력하는 프로그램을 작성하라. 단, 이동 횟수는 최소가 되어야 한다.
아래 그림은 원판이 5개인 경우의 예시이다.

입력
첫째 줄에 첫 번째 장대에 쌓인 원판의 개수 N (1 ≤ N ≤ 20)이 주어진다.
출력
첫째 줄에 옮긴 횟수 K를 출력한다.
두 번째 줄부터 수행 과정을 출력한다. 두 번째 줄부터 K개의 줄에 걸쳐 두 정수 A B를 빈칸을 사이에 두고 출력하는데, 이는 A번째 탑의 가장 위에 있는 원판을 B번째 탑의 가장 위로 옮긴다는 뜻이다.
조건
- 시간 제한 : 1s
- 메모리 제한 : 256MB
해설
4개짜리 하노이탑을 예시로 생각해보면, 아래와 같다.
1→2 로 3개의 원판을 옮기고, 1→3 로 4번째 원판을 옮긴 뒤 2→3 로 3개의 원판을 옮긴다. N=3의 경우에는 똑같이 1→3 로 2개의 원판을 옮기고, 1→2 로 3번째 원판을 옮긴 뒤 3→2 로 2개의 원판을 옮긴다. 원판이 하나일 경우에는 그대로 옮겨준다. 이 과정에서 원판을 옮기는 순서대로 출력해주면 된다.
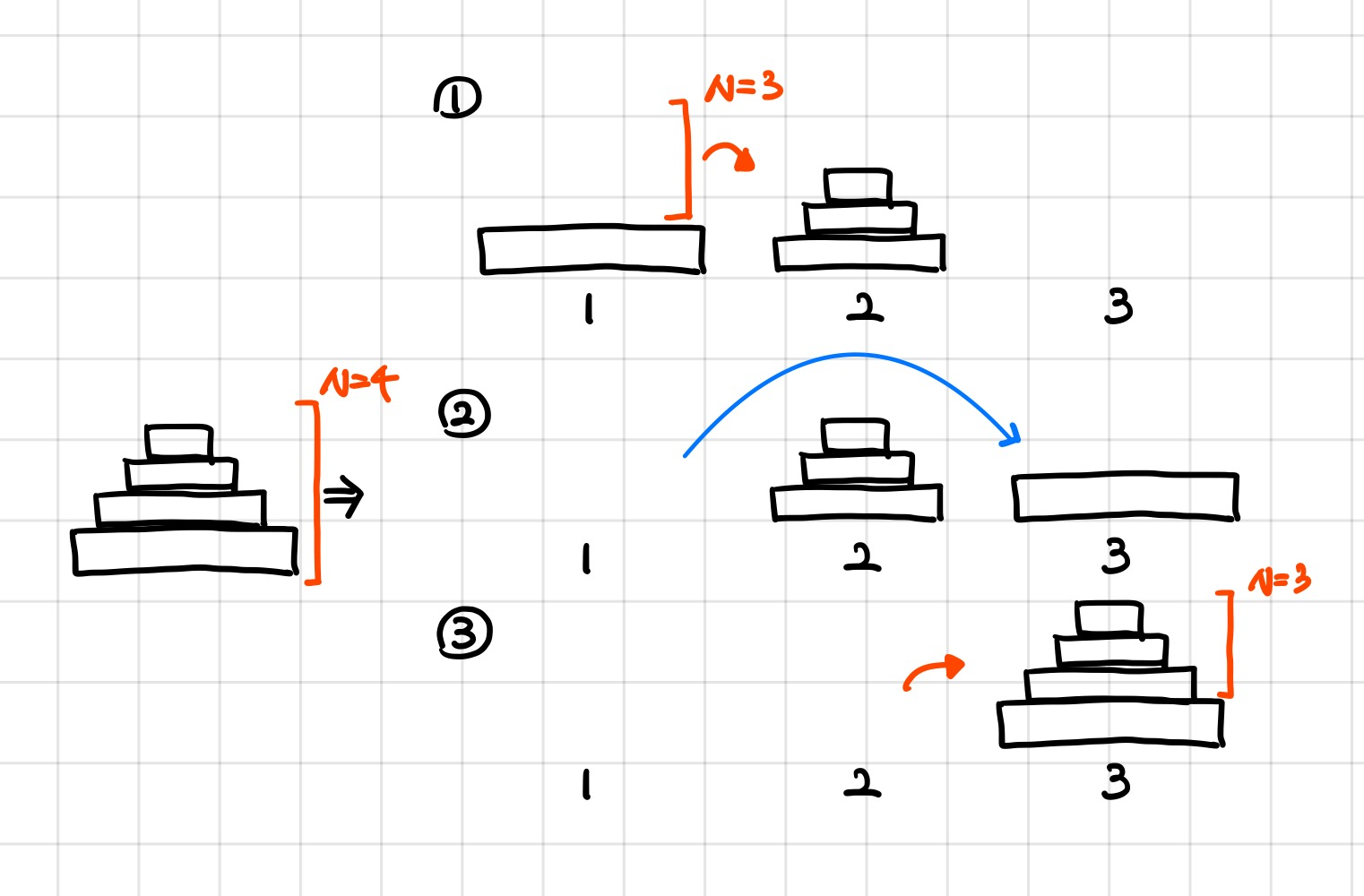
위 내용을 재귀를 이용해 구현해주면 된다.
풀이
반복해서 규칙적으로 움직이는 값이 많으므로 재귀를 이용해 해결해주었다. 이를 위해 tower 함수를 만들어주었다. N 값에 따라서 출발 / 도착지가 달라지기 때문에, 인자로 출발 위치, 도착 위치, N 값을 받아주어 tower(int from, int to, int N)의 형태로 선언해주었다.
해설에서 설명했던 것 처럼, 1→3으로 원판들을 옮기고자 한다면 N-1까지의 원판은 1→2로 옮기고, N번째 원판을 1→3으로 옮긴 뒤 N-1까지의 원판을 다시 2→3으로 옮겨야 한다. 출발지와 도착지가 딱 정해져있지 않지만, 분명한 것은 N까지 원판을 옮기고자 하는 위치를 피해 N-1까지의 원판을 옮겨야 한다는 것이다. 출발지와 도착지를 제외한 칸은 선택하기 위해 남은 한 칸의 위치는 6-from-to로 구해주었다. 여기에서 각 함수에서 출력해줄 부분은 N번째 원판의 움직임이다. N=1인 경우에는 중간 과정이 없으므로 재귀 호출하지 않고 들르는 곳 없이 한번에 움직여준다.
void tower(int from, int to, int N) {
if(N == 1) {
cout << from << " " << to << '\n';
} else {
tower(from, 6-from-to, N-1);
cout << from << " " << to << '\n';
tower(6-from-to, to, N-1);
}
}
하노이 탑의 최소한으로 움직이는 횟수는 2^N-1과 같으므로 해당 값을 만들어 출력해주고, N개의 원판이 1에서 3으로 움직이는 과정을 출력해주기 위해 tower(1, 3, N)을 실행해주면 원하는 결과를 얻을 수 있다.
int main() {
int N, K = 1;
cin >> N;
for(int i = 0; i < N; i++) { K *= 2; }
cout << K-1 << '\n';
tower(1, 3, N);
return 0;
}코멘트
이정도면 할 만 하지!
고민
고민고민하지마
코드
#include <iostream>
using namespace std;
void tower(int from, int to, int N) {
if(N == 1) {
cout << from << " " << to << '\n';
} else {
tower(from, 6-from-to, N-1);
cout << from << " " << to << '\n';
tower(6-from-to, to, N-1);
}
}
int main() {
int N, K = 1;
cin >> N;
for(int i = 0; i < N; i++) { K *= 2; }
cout << K-1 << '\n';
tower(1, 3, N);
return 0;
}
Uploaded by Notion2Tistory v1.1.0