문제링크
https://www.acmicpc.net/problem/12865
문제
이 문제는 아주 평범한 배낭에 관한 문제이다.
한 달 후면 국가의 부름을 받게 되는 준서는 여행을 가려고 한다. 세상과의 단절을 슬퍼하며 최대한 즐기기 위한 여행이기 때문에, 가지고 다닐 배낭 또한 최대한 가치 있게 싸려고 한다.
준서가 여행에 필요하다고 생각하는 N개의 물건이 있다. 각 물건은 무게 W와 가치 V를 가지는데, 해당 물건을 배낭에 넣어서 가면 준서가 V만큼 즐길 수 있다. 아직 행군을 해본 적이 없는 준서는 최대 K만큼의 무게만을 넣을 수 있는 배낭만 들고 다닐 수 있다. 준서가 최대한 즐거운 여행을 하기 위해 배낭에 넣을 수 있는 물건들의 가치의 최댓값을 알려주자.
입력
첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)가 주어진다.
입력으로 주어지는 모든 수는 정수이다.
출력
한 줄에 배낭에 넣을 수 있는 물건들의 가치합의 최댓값을 출력한다.
조건
- 시간 제한 : 2s
- 메모리 제한 : 512MB
해설
전형적인 배낭문제의 기본형 문제이다. 경우를 따져서 최적의 방법을 찾으면 된다. 자세한 내용은 풀이에서 서술하겠다.
풀이
주어지는 값은 물건의 개수 N, 가방에 담을 수 있는 물건의 최대 무게 K, 각 물건의 무게 w 와 가치 v 이다. 아래 그림과 같이 표현하기 위해 N+1의 크기를 갖는 물건 벡터 things, 0으로 초기화된 2차원 벡터 DP[N+1][K+1]을 선언해준다. 이를 코드로 표현하면 아래와 같다. things와 같이 무게와 가치를 갖는 물건을 입력받았다고 가정하자.

물건의 무게와 가치를 한번에 다루기 위해 thing 구조체를 선언해주었다.
struct thing {
int w;
int v;
};
이를 이용해 입력 및 선언 코드를 작성하면 아래와 같다.
int N, K;
cin >> N >> K;
vector<thing> things(N+1);
for(int i = 1; i <= N; i++) {
thing temp;
cin >> temp.w >> temp.v;
things[i] = temp;
}
vector<vector<int>> DP(N+1, vector<int>(K+1, 0));
이해를 위해 그림과 함께 길게 서술하였고, 아래에 핵심을 요약해두었습니다!
아래 그림 상의 DP 2차원 벡터의 세로가 담을 수 있는 물건의 개수, 가로가 담을 수 있는 총 무게라고 하자. 물건을 아무것도 담지 않았을 때, 물건의 총 무게가 0일때는 가방에 담겨있는 물건이 아무것도 없으므로 총 가치는 0이 된다. 그 의미로, 0의 행 / 0의 열에는 0으로 초기화되어있다.
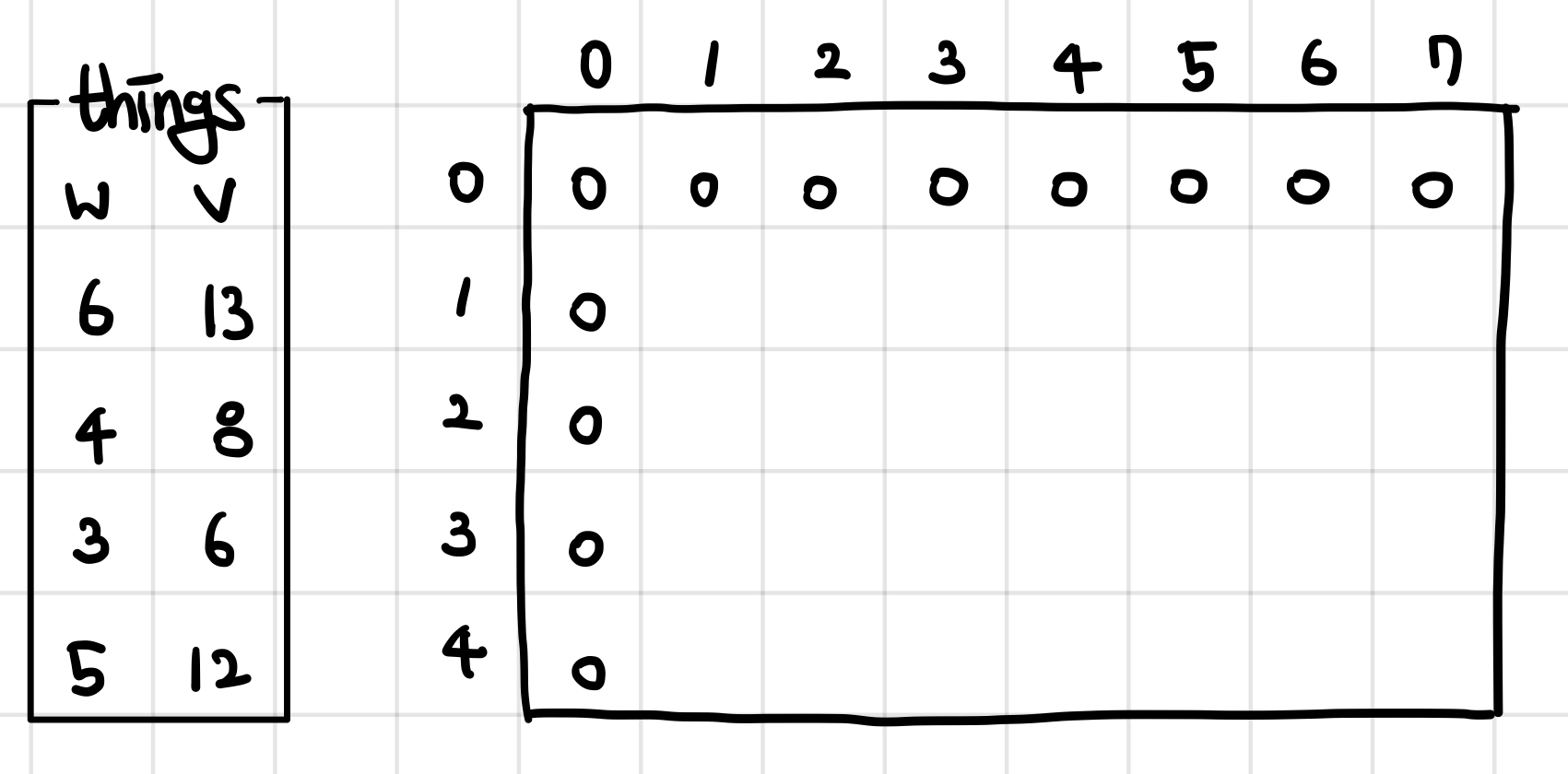
첫번째 물건(무게가 6 / 가치가 13)을 집어넣는다고 할 때, 해당하는 무게 6이 되기 전까지는 아무것도 담지 않았을 때와 물건의 총 가치가 같다. 따라서, 파란색으로 표시해둔 것처럼, 6 이전의 가치는 이전 단계의 값을 그대로 가져온다. 총 무게가 6보다 크거나 같을 때는 해당 물건을 담을 수 있으므로 가치를 추가해주어야 한다. 이때, 총 무게가 6인 경우에는 무게가 0일 때의 가방에 무게가 6인 물건을 추가하는 것과 같고, 총 무게가 7인 경우에는 무게가 1일 때의 가방에 무게가 6인 물건을 추가하는 것과 같다. 빨간 테두리를 친 값에 물건의 가치를 더한 값을 저장해준다.

2개의 물건을 담을 수 있다고 할 때, 무게가 4이고 가치가 8인 물건을 담는다고 해보자. 첫번째 물건과 똑같은 방식으로 총무게가 4보다 작은 경우 해당 무게에 대한 이전 단계의 가치를 그대로 가져온다. 총 무게가 4와 같거나 큰 경우에는 무게가 4인 물건을 넣기 전에 있던 가치를 가져와 비교하고나서 넣을 지 말지를 결정해야 한다. 총 무게가 4, 5인 경우에는 물건을 담았을 때의 가치가 8이 되기 때문에 8을 저장한다. 총 무게가 6, 7인 경우에는 총 무게가 2, 3일 때의 가치에 물건의 가치 8을 더한 값보다 무게가 6인 물건을 넣었을 때의 가치가 더 크므로, 더 큰 경우의 가치를 가져와 저장해준다.
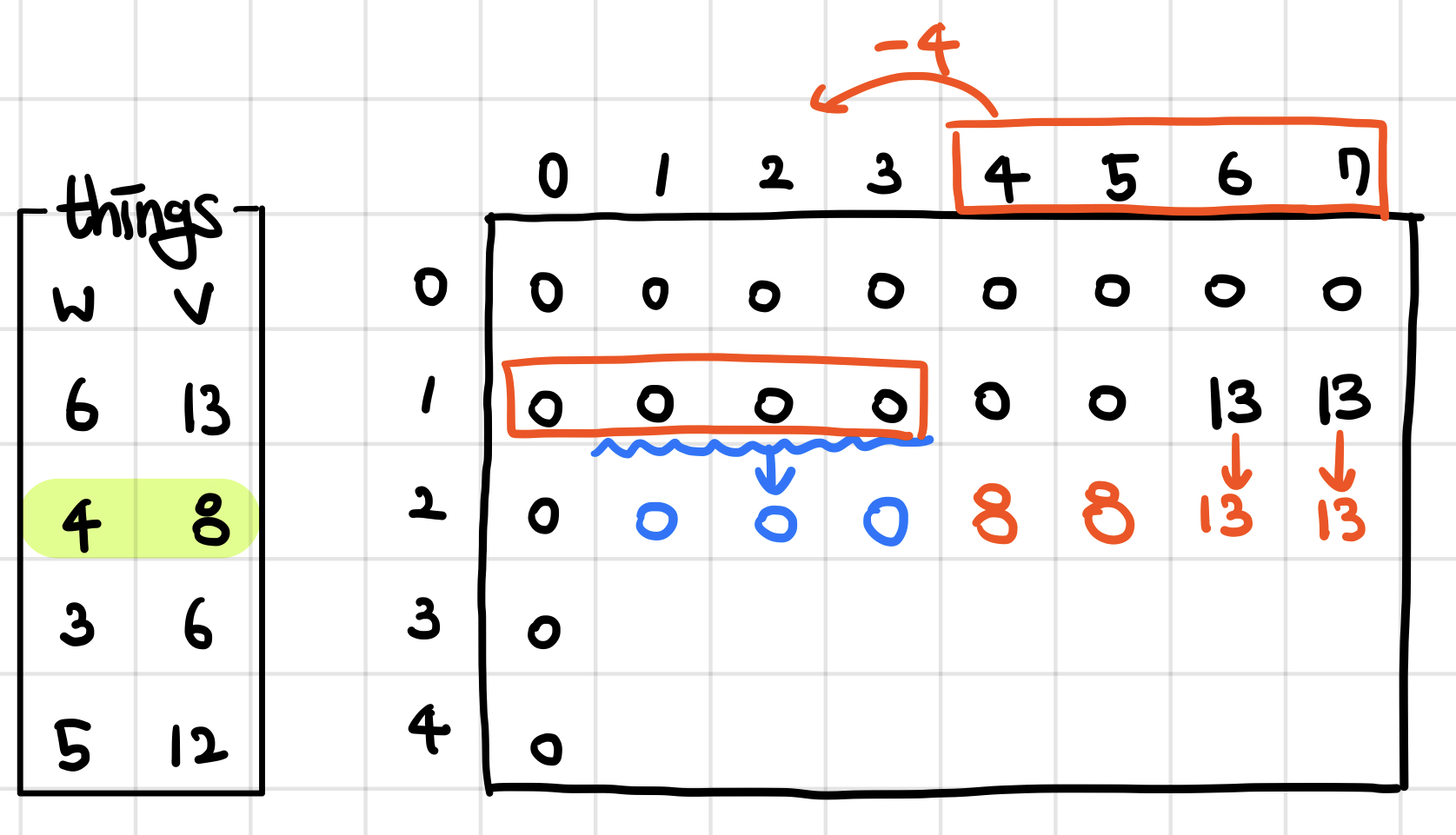
같은 방식으로 나머지 물건에 대해서도 경우를 따져준다.
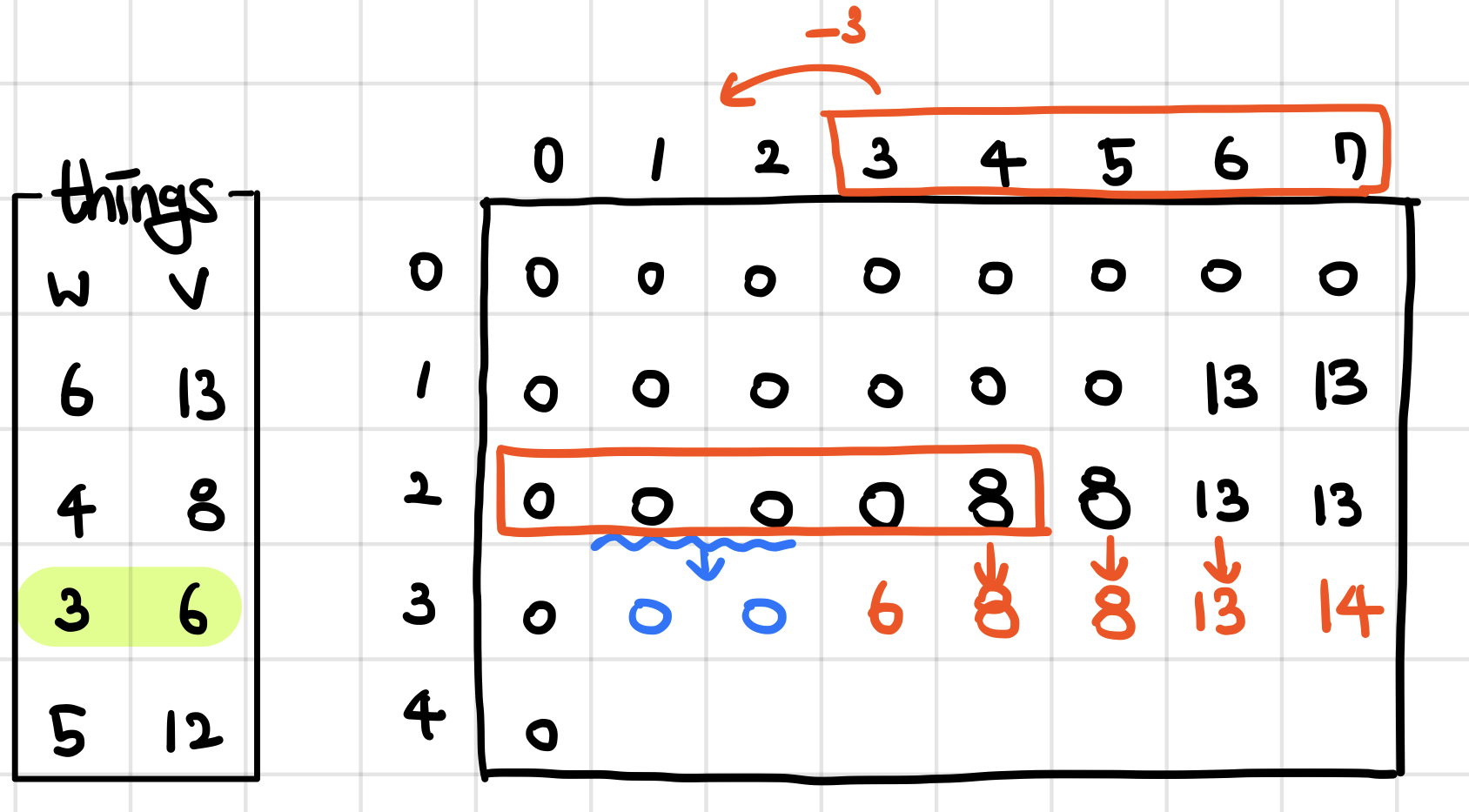

핵심적인 내용은 아래와 같다.
- 현재 계산 중인 가방의 총 무게가 물건 무게보다 크거나 같은가?
- true → 현재 담을지 고민하는 물건을 담았을 때의 가치가 담지 않았을 때의 가치보다 큰가?
- true → 물건을 담았을 때의 가치를 저장
- false → 물건을 담지 않았을 때의 가치를 저장
- false → 물건을 담지 않았을 때의 가치를 저장 (이전 물건을 고려할 때의 가치 그대로)
- true → 현재 담을지 고민하는 물건을 담았을 때의 가치가 담지 않았을 때의 가치보다 큰가?
각 물건에 대해서, 0~최대 가방의 무게에 대해 위 알고리즘을 적용하면 마지막에는 얻을 수 있는 최대 가치가 저장되어 있다. 이를 출력하면 원하는 결과를 얻을 수 있다. 그리고 이를 코드로 옮기면 아래와 같다.
for(int i = 1; i <= N; i++) {
for(int j = 1; j <= K; j++) {
int wi = things[i].w;
int vi = things[i].v;
if(wi > j) {
DP[i][j] = DP[i-1][j];
} else {
DP[i][j] = max(DP[i-1][j], vi + DP[i-1][j-wi]);
}
}
}
cout << DP[N][K];코멘트
생각보다 되게 이해하기 헷갈렸던 알고리즘. 그래서 일부러 그림까지 그려봤다. 저렇게 정리해두니 한결 이해하기가 편안한 것 같네. 이 문서는 편집해서 따로 저장해둬야겠다.
코드
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
struct thing {
int w;
int v;
};
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int N, K;
cin >> N >> K;
vector<thing> things(N+1);
for(int i = 1; i <= N; i++) {
thing temp;
cin >> temp.w >> temp.v;
things[i] = temp;
}
vector<vector<int>> DP(N+1, vector<int>(K+1, 0));
for(int i = 1; i <= N; i++) {
for(int j = 1; j <= K; j++) {
int wi = things[i].w;
int vi = things[i].v;
if(wi > j) {
DP[i][j] = DP[i-1][j];
} else {
DP[i][j] = max(DP[i-1][j], vi + DP[i-1][j-wi]);
}
}
}
cout << DP[N][K];
return 0;
}





Uploaded by Notion2Tistory v1.1.0