이산 시간 푸리에 급수
이산 신호와 샘플링
이산시간 신호 $x[n]$ 은 정수 시점에만 값을 가진다. 이렇게 대괄호를 이용해서 이산 신호임을 표현할 수 있다.
샘플링은 연속 신호를 일정한 시간 간격 $T$ 마다 값을 측정한 것을 말한다. 원본은 연속신호라고 하더라도 MCU 에서처럼 실제로 데이터를 처리하기 위해서는 연속신호를 일정한 주기마다 측정해 이산신호로 변환하여 사용한다.
이산시간 푸리에 급수
Discrete Time Fourier Series
이산시간 푸리에급수는 정수 주기 N을 가지는 신호이다. 연속시간 푸리에의 수식과 유사하지만, 주기와 값이 있는 시점이 항상 정수라는 것이 차이점이다.
이산 시간의 푸리에 급수는 아래와 같은 식을 가진다.
$$
x_N[n] = \sum_{k=0}^{N-1}a_ke^{jk\frac{2\pi}{N}n}
$$
연속시간 푸리에 급수와 꽤 유사한 형태를 가지는데, 기존의 주파수 $\omega$ 를 $\frac{2\pi}{N}$ 으로 표현한다. ‘이산적임’을 표현하기 위해 함수 신호의 괄호도 [ 이렇게 ] 작성한다. 주기가 N 이기 때문에, k가 움직이는 범위는 0~N-1 이면 충분하다. (연속된 N개의 신호만 사용한다)
만약 $k=1$ 이라면 $e^{j\frac{2\pi}{N}n}$, $k=N+1$ 이라면 $e^{j(N+1)\frac{2\pi}{N}n} = e^{j\frac{2\pi}{1}n + j\frac{2\pi}{N}n} = e^{j\frac{2\pi}{1}n + j\frac{2\pi}{N}n} = e^{j\frac{2\pi}{N}n}$ 의 순서로 식을 정리해서 결국 복소지수가 $k=1$ 일 때와 동일해진다. 그런데 위처럼 푸리에 급수로 표현할 때는 유일한 복소지수 성분으로 얼마나 해당 성분이 포함되어있는지를 파악하기 위해 사용하는 것인데 동일한 성분이 굳이 2번 이상 들어갈 필요가 없으므로 하나의 주기를 벗어나는 신호는 제외해준다. (0~N-1 만 더함)
푸리에 계수 $a_k$ 찾기
위 식에서 $a_k$를 유도해보자.
r번째 basis (복소지수) 로 신호들을 내적하는 상황을 생각해보자. 양변에 동일하게 N개의 신호에 대해 내적을 수행하도록 연산을 추가해준다.
$$
x_N[n] = \sum_{k=0}^{N-1}a_ke^{jk\frac{2\pi}{N}n}\
\sum_{n=0}^{N-1}x_N[n]\cdot e^{-jr\frac{2\pi}{N}n} = \sum_{n=0}^{N-1}\sum_{k=0}^{N-1}a_ke^{jk\frac{2\pi}{N}n}\cdot e^{-jr\frac{2\pi}{N}n}\
=\sum_{n=0}^{N-1}\sum_{k=0}^{N-1}a_ke^{j\frac{2\pi}{N}n(k-r)}
$$
여기에서 $k=r$ 인 경우와 $k\neq r$ 인 경우로 나눠서 생각해볼 수 있다.
우선 $k=r$ 인 경우
$$
\sum_{n=0}^{N-1}\sum_{k=0}^{N-1}a_ke^{j\frac{2\pi}{N}n(k-r)}\
=\sum_{n=0}^{N-1}a_re^{0}\
=\sum_{n=0}^{N-1}a_r\
=N\cdot a_r
$$
$k\neq r$ 인 경우, $k=r+1$ 이라고 하자.
$$\sum_{n=0}^{N-1}\sum_{k=0}^{N-1}a_ke^{j\frac{2\pi}{N}n(k-r)}\\
= \sum_{n=0}^{N-1}a_{r+1}e^{j\frac{2\pi}{N}n}\\
= a_{r+1}\sum_{n=0}^{N-1}e^{j\frac{2\pi}{N}n}\\
= 0$$
이때, 주기가 N이고 N개의 신호를 모두 더하고 있으므로, 복소평면 위를 생각해봤을 때, 신호의 총합은 원점에 있다. 따라서 $\sum$ 의 결과가 0이 된다.

그러면 $k=r$ 인 경우에만 유효하게 값이 남으므로, 아래처럼 수식을 정리할 수 있다.
$$
\sum_{n=0}^{N-1}x_N[n]\cdot e^{-jr\frac{2\pi}{N}n} = N\cdot a_r
\
a_r = \frac{1}{N}\cdot\sum_{n=0}^{N-1}x_N[n]\cdot e^{-jr\frac{2\pi}{N}n}
$$
이산시간 푸리에 변환
이제 이산시간 푸리에 변환을 적용해보자. 시그마의 밑에 $n=$ 이라고 표기된 것은 “N개의 연속된 n에 대해서” 라는 의미이다.
$$
N\cdot a_r = \sum_{n=}x_N[n]\cdot e^{-jr\frac{2\pi}{N}n}
$$
이제 기호의 편의를 위해 $\frac{2\pi}{N}$을 $\Omega_0$이라고 하자. $\Omega_0$ 을 축으로 두면 $2\pi$ 를 주기로 갖게된다.
만약 위 식에서 주기 $N\rightarrow\infty$ 로 보내면 어떤 변화가 생기냐
- 주기가 무한이므로 더이상 $x$ 는 주기를 가지지 않는 비주기 함수가 된다. $x[n]$
- $a_kN = X(\frac{2\pi}{N}k) = X(k\Omega_0)$ 으로 치환을 하자. $X$는 원래 주파수 도메인…$\frac{2\pi}{N}$ 이 주파수의 역할을 한다.
- $k\cdot \frac{2\pi}{N}$를 쪼개보면 $k$는 0~
$N-1$ 의 범위에서 움직이고 $\frac{2\pi}{N}$는 0으로 수렴하게 된다. 그래서 $k\cdot \frac{2\pi}{N}$는 $0$~$2\pi$ 사이에서 실수값으로 움직이게 된다. (0과 $2\pi$ 사이에서 모든 실수를 나타낼 수 있다) - 0과 $2\pi$ 사이를 움직이는 값을 $\Omega$ 라고 하자.
그러면 이걸 식으로 옮기면
$$\lim_{N\rightarrow\infty}X(a_k\cdot N) = \lim_{N\rightarrow\infty}\sum_{n} x_N[n]e^{-jk\frac{2\pi}{N}n}\\\lim_{N\rightarrow\infty}X(\Omega) = \lim_{N\rightarrow\infty}\sum_{n=0}^{N-1} x[n]e^{-j\Omega n}$$
이렇게 정리가 되면 우변이 리만합으로 적분을 할 수 있을 것 같지만, 밑변이 1을 유지하고 좌우로 넓어지는 형태이기 때문에 적분으로 변환할 수는 없는 수식이다.
결국 위 식을 아래 수식처럼 정리가 된다.
$$
X(\Omega) = \sum_{n=-\infty}^{\infty}x[n]e^{-j\Omega n}
$$
위 형태가 이산시간에서의 푸리에 변환이라고 볼 수 있다.
이산시간 푸리에 역변환
이산시간에서의 푸리에 역변환을 유도해보자.
우선 기존의 이산신호에 대한 푸리에 급수 수식을 확인해보면 아래와 같다.
$$
x_N[n] = \sum_{k=}a_ke^{jk\frac{2\pi}{N}n}
$$
여기에서 테크닉을 적용하기 위해 우변에 $2\pi$, N 을 곱하고 나누면서 아래 수식처럼 정리할 수 있다.
$$
x_N[n] = \frac{1}{2\pi}\sum_{k=}Na_ke^{jk\frac{2\pi}{N}n}\cdot \frac{2\pi}{N}
$$
여기에서 양 변에 $N\rightarrow\infty$ 를 취하면
$$
\lim_{N\rightarrow\infty} x_N[n] = \lim_{N\rightarrow\infty}\frac{1}{2\pi}\sum_{k=}Na_ke^{jk\frac{2\pi}{N}n}\cdot \frac{2\pi}{N}\
x[n] = \lim_{N\rightarrow\infty}\frac{1}{2\pi}\sum_{k=}X(k\Omega_0)e^{jk\Omega_0n}\cdot \frac{2\pi}{N}
$$
여기에서 $N\rightarrow\infty$ 의 상황에서 $X(k\Omega_0)e^{jk\Omega_0n}$ 가 함수값, $\frac{2\pi}{N}$가 너비를 의미한다고 생각하면 리만합을 통한 적분을 적용할 수 있다.
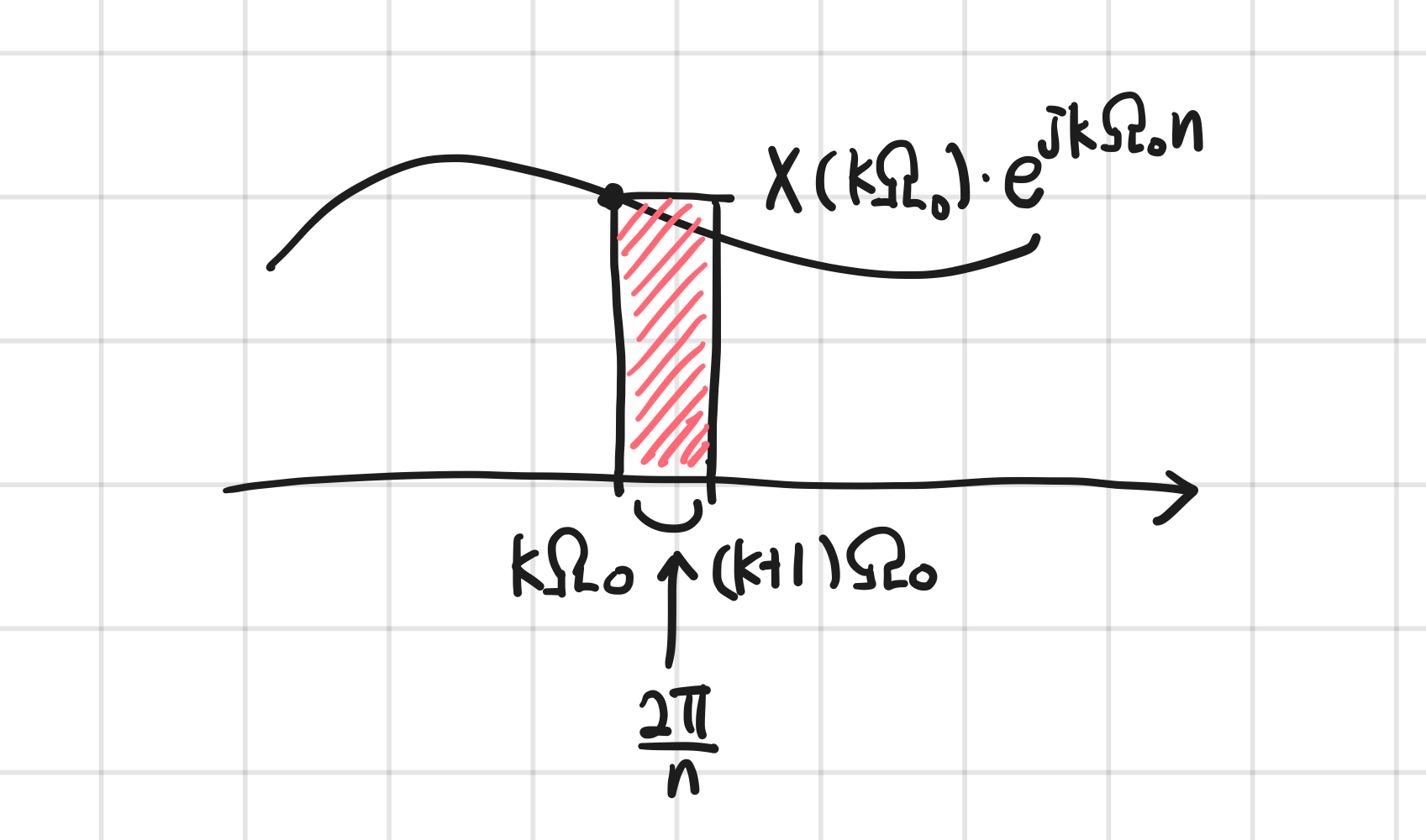
그러면 푸리에 변환을 이렇게 표현할 수 있다.
$$
x[n] = \frac{1}{2\pi}\int_0^{2\pi}X(\Omega)\cdot e^{j\Omega n}d\Omega
$$
그리고 푸리에 역변환에 대해서는 이렇게 표현을 할 수 있다.
$$
X(\Omega)=\sum_{n=-\infty}^\infty x[n]\cdot e^{-j\Omega n}
$$
샤라웃
https://www.youtube.com/playlist?list=PL_iJu012NOxcDuKgSjTKJZJd3bQtkAyZU
혁펜하임의 “퍼펙트” 신호 및 시스템 (Signals & Systems)
수백명의 A+를 배출한 미친 강의!
www.youtube.com
'Embedded System > 신호 및 시스템' 카테고리의 다른 글
| [신호및시스템] Phase 3-3 - Fast Fourier Transform (0) | 2025.10.07 |
|---|---|
| [신호및시스템] Phase 3-2 - 이산 푸리에 변환 (0) | 2025.10.07 |
| [신호및시스템] Phase 2-3 - 주파수 도메인 분석 - 함수의 푸리에 변환 적용 (0) | 2025.10.04 |
| [신호및시스템] Phase 2-2 - 주파수 도메인 분석 - 푸리에 변환 (0) | 2025.10.04 |
| [신호및시스템] Phase 2-1 - 주파수 도메인 분석 - 푸리에 급수 (0) | 2025.09.28 |





