디지털 신호처리 파이프라인
앞서 수행한 ADC + DAC 를 합쳐서 보면 아래와 같은 순서로 진행됨을 알 수 있다.

ㅤ
에어팟의 노이즈캔슬링 기능을 구현한다고 해보자. 이때 마이크로 들어오는 노이즈 섞인 노래 입력이 $x(t)$, 에어팟으로 나가는 출력을 $y(t)$ 라고 한다면.
- 에어팟으로 음악 소리를 입력받는다. ($x(t)$)
- Impulse train을 곱해 $T_0$를 주기로 하는 신호 그래프로 만든다.
- 신호를 골라내어 $x[n]$ 시퀀스로 만든다.
- 디지털로직을 적용해, 변환 과정을 거친다. 이때 변환된 시퀀스는 $y[n]$ 이 된다.
- 시퀀스 $y[n]$을 다시 impulse train 그래프로 만든다.
- 시퀀스를 다시 아날로그 신호로 만들기 위해서 LPF를 통과시켜 $y(t)$ 를 만든다.
- 스피커로 소리 출력
ㅤ
중간에 $H_d(\Omega)$ 의 디지털 필터를 거치도록 파이프라인이 구성되어있다. 만약 단순히 아날로그 필터를 배치하더라도 동작에 크게 문제는 없을 것이다. (왜나면 역할은 같으니깐.) 그러나 복잡한 상황에서 조건에 따라 다르게 동작하는 필터를 적용하고 싶다면 디지털 필터의 사용이 훨씬훨씬 유리하다.
ㅤ
이 파이프라인은 CTFT와 DTFT의 관계를 보여준다.

ㅤ
여기에서 연속신호 $x(t)$ 에서부터 출력 연속신호 $y(t)$ 까지의 수식을 나열하면 다음과 같다.
$$
x(t)\\
x(t)\rightarrow x_p(t)
\\X_p(\omega)\rightarrow X_d(\Omega) \X_d(\Omega) = X_d(\omega T)\\
Y_d(\Omega) = X_d(\Omega) \cdot H_d(\Omega)\\
Y_d(\omega T) = X_d(\omega T) \cdot H_d(\omega T)\\
Y(\omega) = X(\omega) \cdot H_d(\omega T)\\
y(t)
$$
- 신호로 들어온 $x(t)$ 에 impulse train을 곱한 $x_p(t)$ 신호를 푸리에 변환하여 샘플링된 연속 신호에 대한 푸리에 변환 $X_p(\omega)$ 를 구한다.이때, $x(kT_0)$는 $x[k]$ 라고 봐도 무방하므로, $X_p(\omega)$ 는 $X_d$ 라고 봐도 무방하다. 여기에서 $\omega T_0 = \Omega$ 로 정규화된 각주파수 형태로 변환까지 해준다면 아래처럼 수식을 변경할 수 있다.
- $$
X_p(\omega) \approxeq \sum_{k=-\infty}^\infty x[k] e^{-j\Omega k} = X_d(\Omega) = X_d(\omega T)
$$ - $$
X_p(\omega) = \int_{\infty}^{\infty}x(t)\sum_{k=-\infty}^\infty\delta(t-kT_0)\cdot e^{j\omega t}dt\\
= \int_{\infty}^{\infty}\sum_{k=-\infty}^\infty x(kT_0)\delta(t-kT_0)\cdot e^{j\omega kT_0}dt\\
= \sum_{k=-\infty}^\infty x(kT_0) e^{-j\omega kT_0}
$$ - 샘플링된 이산 신호의 푸리에 변환 $X_d$ 에 디지털 필터인 $H_d$ 를 적용한다.
- $$
X_d(\Omega)\cdot H_d(\Omega) = Y_d(\Omega)
$$ - $Y_d(\Omega)$ 에 LPF를 적용해, 연속 함수 $Y(\omega)$ 의 형태로 복원한다.
- 이를 다시 역푸리에 변환을 적용하면 출력신호 $y(t)$ 를 얻을 수 있다.
ㅤ
여기에서 전체 과정을 $H(\omega)$ 라고 볼 때, 이걸 등가 아날로그 시스템이라고 생각한다면 아래 처럼 축소할 수 있다. 여기에서는 $H$ 를 하나의 아날로그 필터로서 바라보는 관점.
$$
X(\omega)\rightarrow H(\omega)\rightarrow Y(\omega)
$$
ㅤ
디지털 신호의 푸리에 변환에 대해서 적용했던 $H_d(\Omega)$ 와 $H_d(\omega T)$ 가 동일하다면 앞서 살펴본 실제 디지털 처리 과정과 아날로그 신호 관점에서의 과정이 동일한 output을 낸다고 볼 수 있다.
- $H_d(\Omega)$ 는 $x[n] \rightarrow y[n]$ 을 담당 … 디지털 주파수 $\Omega$ 에 대해서 얼마나 닮았는가?
- $H(\omega)$ 는 $x(n) \rightarrow y(n)$ 을 담당 … 아날로그 주파수 $\omega$ 에 대해서 얼마나 닮았는가?
- 아날로그 신호를 디지털 신호로 변환하더라도 동일한 정보를 가지고 있기 때문에, 샘플링과 복원 과정이 이상적으로 수행될 때 $H$와 $H_d$ 변환이 동일하다면 결과도 동일함.
ㅤ
따라서 위 파이프라인을 거치는 연산을 길고 복잡한 디지털 신호에 대한 처리로 생각하는 대신에 단순히 아날로그 신호 관점에서 $Y(\omega) = X(\omega)\cdot H(\omega)$ 를 이용해도 된다. 이 말은, 디지털 처리 과정을 거쳤지만 $x(t)$ 에서 아날로그 필터를 거쳐 $y(t)$ 를 얻었다고 볼 수 있다는 것이다!!
ㅤ
즉, 위 디지털 필터링 과정을 아래같은 아날로그 필터링을 적용하는 것과 동일하다고 봐도 무방하다!
$$
Y(\omega) = X(\omega)\cdot H(\omega)
$$
ㅤ
다만, 여러가지 이슈로 인해서 완전하고 완벽하고 이상적으로 샘플링과 복원을 수행할 수 없기 때문에 완벽하게 디지털 변환과 아날로그 변환 간의 등식이 성립하지는 않는다.
- LPF 필터가 정확하게 구간이 딱 칼같이 나뉘지는 않는다.
- 샘플링 간격이 정확하게 $T$ 가 아닐 수 있다.
- Impulse Train을 이론처럼 만들 수 없다.
- 처리를 위해서는 시간 지연이 발생할 수 있다.
- 기타 둥둥
ㅤ
이산 시간 샘플링
Downsampling
샘플의 개수를 줄이기.
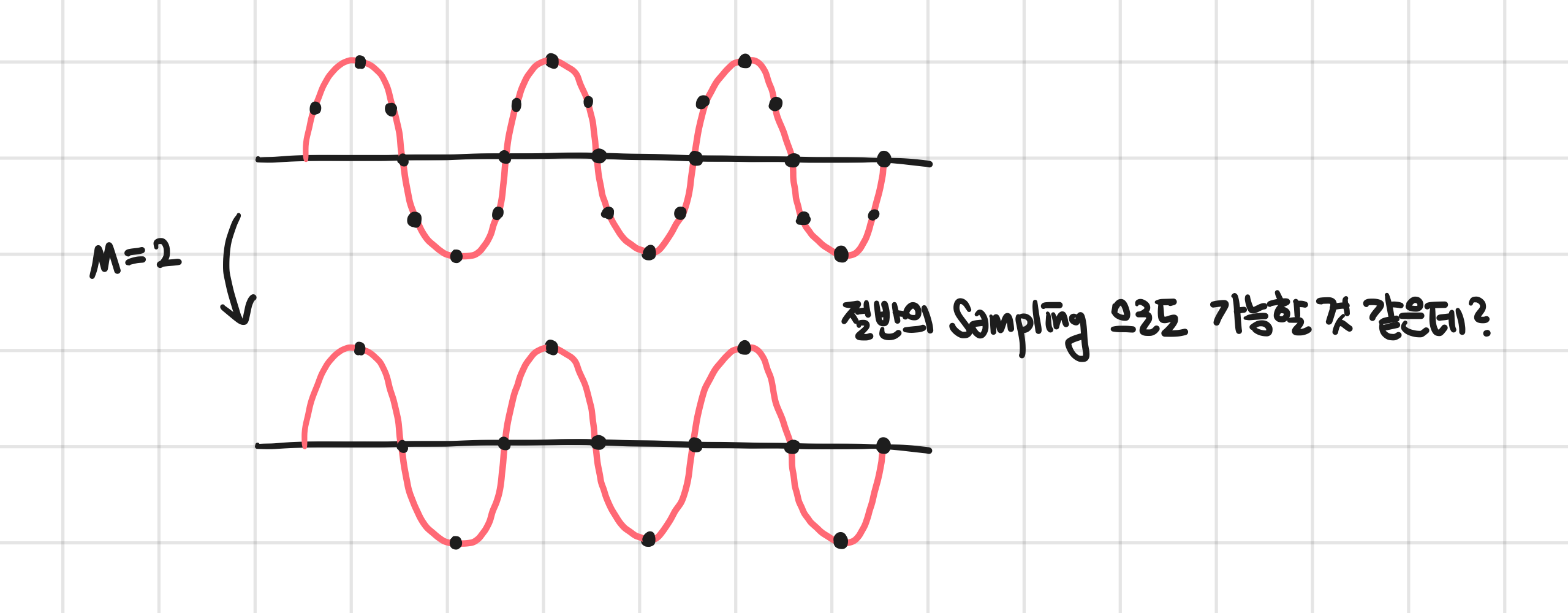
M=5 로 다운샘플링 한다는 것은 5개의 샘플 중에서 1개만 선택한다는 의미이다. (M은 downsampling factor)
ㅤ
다운샘플링을 통해서 연산이 필요한 샘플 숫자를 줄이고 샘플링 주파수를 감소시켜 메모리나 처리 연산의 비용을 줄일 수 있다.
ㅤ
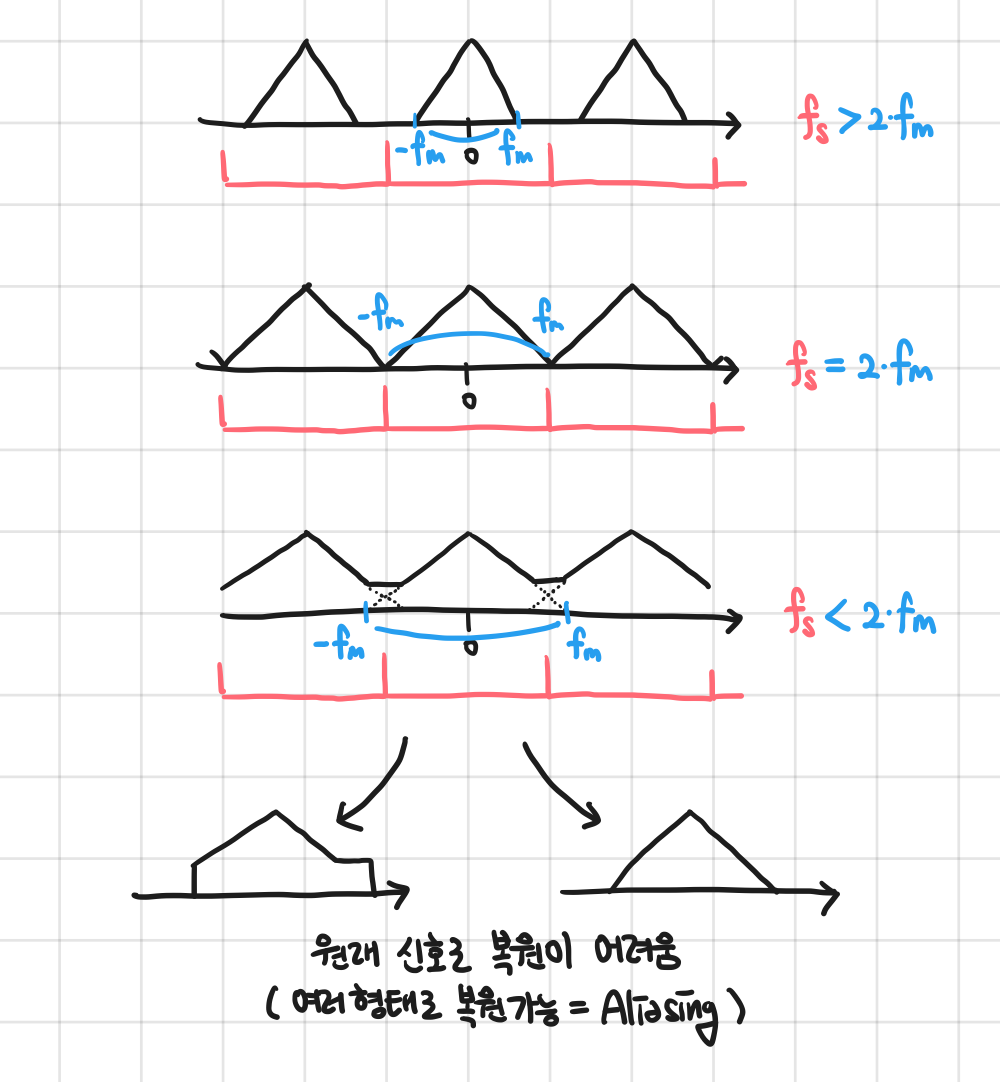
다만, 샘플링 주파수의 감소로 인해 (나이퀴스트 조건의 위반으로) Aliasing 의 발생 가능성이 있다.
나이퀴스트 이론
샘플링 주파수 $f_s ≥ 2 × f_{max}$ 를 지키지 않으면 aliasing이 발생한다.
ㅤ
Decimation
LPF + Downsampling
미리 고주파 영역들을 잘라내어서 $f_{max}$ 부분들을 샘플링 주파수 이하로 줄여준 다음에 Downsampling을 적용해서 Aliasing이 발생하지 않도록 하기.

ㅤ
Upsampling
샘플의 개수 늘리기.
신호 사이에 신호값 0을 넣어서 일부러 샘플의 개수를 늘려줄 수 있다. 이를 통해 샘플링 주파수의 증가가 가능하다.
다만 신호의 추가로 인해 의미없는 고주파 성분들이 생길 수 있어서 LPF 필터를 통해 고주파를 제거해준다.

ㅤ
나는 업샘플링은 도대체 어디에 쓰나… 싶었는데, 10kHz를 필요로 하는 시스템에 1kHz 의 신호가 들어왔다면 이걸 업샘플링을 통해서 10kHz 로 불려줘야지 시스템의 사양을 맞춰주는 용도로 사용할 수 있다고 한다. 이 경우에 ‘부드러운 신호 생성 = 보간’ 을 위해 사용하는 것이라 볼 수 있겠다!
'Embedded System > 신호 및 시스템' 카테고리의 다른 글
| [신호및시스템] Phase 5-2 - Z 변환 (0) | 2025.10.18 |
|---|---|
| [신호및시스템] Phase 5-1 - 라플라스 변환 (0) | 2025.10.17 |
| [신호및시스템] Phase 4-2 - 샘플링 복원 (0) | 2025.10.14 |
| [신호및시스템] Phase 4-1 - 샘플링 (0) | 2025.10.14 |
| [신호및시스템] Phase 3-3 - Fast Fourier Transform (0) | 2025.10.07 |





